Why Asians are Good at Chess and Checkers

What does that mean?

A common stereotype in society is that Asians are good at chess. It is simply part of our society, and many people accept it. But why is that? I think I have figured it out. As an Asian that has played chess 3 times total, and lost 3 times, I have figured out exactly why we are so good at chess.

The Important Bit.

You can use a chessboard as a calculator. I know, straight to the point, but that’s just because I don’t feel like writing too much. It takes too much effort to imbed subway surfers in here, so I know fully well I can’t keep your attention spans. But yes, this John Napier guy figured a way to make chessboards into a calculator. Here’s how it works.

Step 1.  Place the first number on the bottom horizontal row.

Step 2.  Place the second number below it in the margin.

Step 3.  Combine all the counters on the bottom horizontal row.

Step 4.  Abbreviate the board from right to left. That is, remove every two counters in a square and place one counter in the square to its left. This process often causes a “chain reaction” that “carries” into squares further to the left, requiring further abbreviation.

Step 5.  The desired answer can now be obtained by converting the abbreviated sum back to a decimal number.

Example: That 116 + 84 = 200 is illustrated below.

WARNING: BIG NUMBERS AHEAD

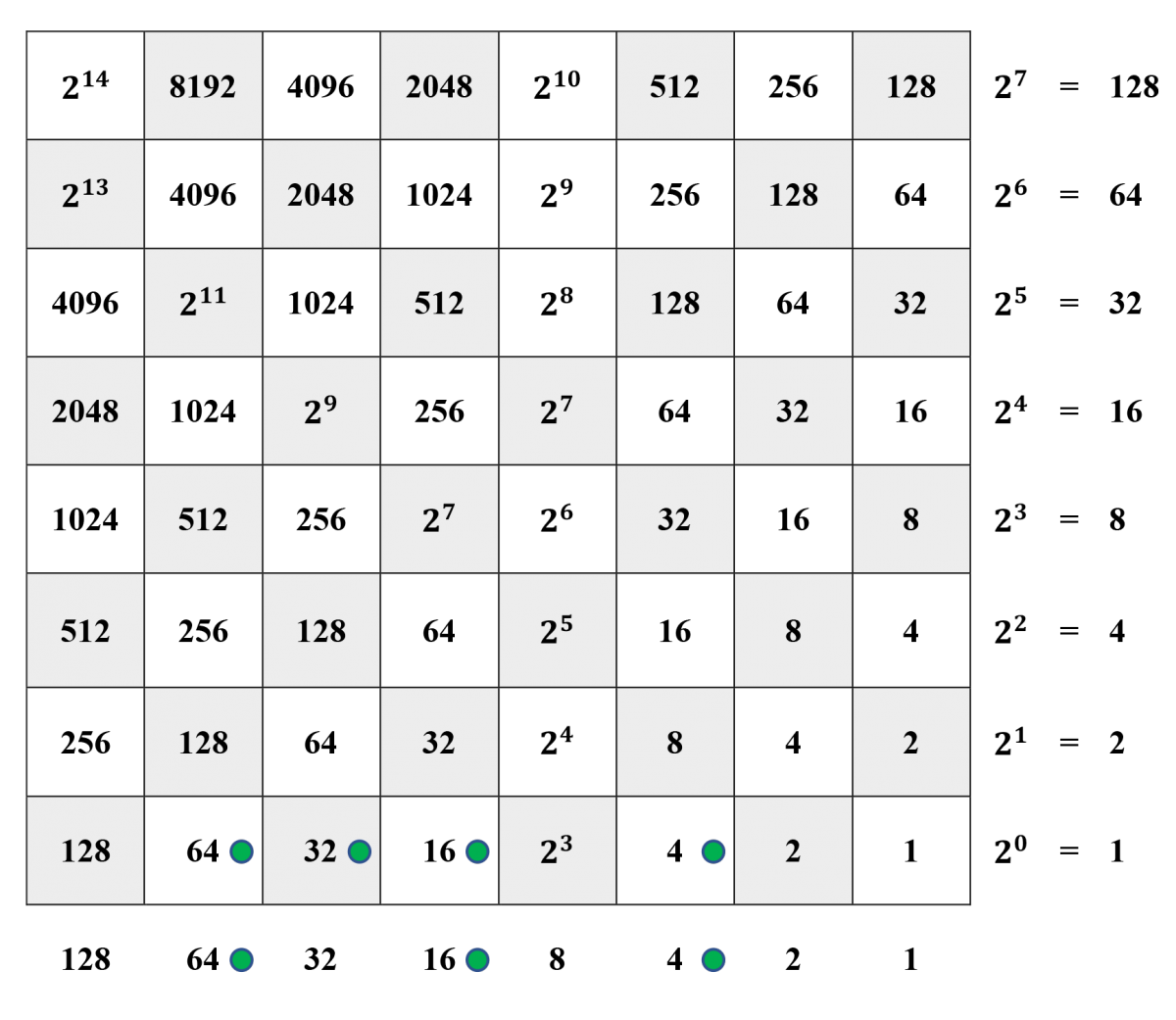
Steps 1 and 2. First 116, decomposed as

116=2^6+2^5+2^4++2^2=64+32+16++4,116=2^6+2^5+2^4++2^2=64+32+16++4, is represented in the bottom horizontal row and

84=2^6++2^4++2^2=64++16++4, 84=2^6++2^4++2^2=64++16++4,is recorded just below it in the margin.

Step 3. Next, all of the counters are combined in the bottom horizontal row.

Step 4. The board is abbreviated in two steps: First, from each square that had two counters after Step 3, one counter is moved to the square to the left and the other is removed. The result is shown above. Second, the abbreviation is repeated: from the square marked “32”, one counter is moved to the left and the other is removed. The result is shown below.

Step 5: Now that each square along the bottom row contains at most one counter, the sum can be read from this row as 116 + 84 = 128 + 64 + 8 = 200.

A Little Self-Awareness.

I’m not an idiot, you 100% took one look, maybe 2, and decided that ain’t worth your time. Good news for you, it wasn’t worth my time either. I just copied and pasted that from another article. I also know you will never use this stupid chessboard calculator, because everyone plays on chess.com and stuff. So why am I here? Because why not. Here’s how to do everything else.

Step 1.  Place the larger number on the bottom horizontal row.

Step 2.  Place the binary complement of the number to be subtracted in the margin below the bottom horizontal row. That is, where there would be a counter in the number itself, leave the square empty; and where there would not be a counter, place one on the square. Do this for all entries from right to left through the highest power of 2 occurring in the decomposition of the larger number.

Step 3.  Combine all the counters on the bottom horizontal row.

Step 4.  Abbreviate the board from right to left; that is, remove every two counters in a square and place one counter in the square to its left. This process often causes a “chain reaction” that “carries” into other squares, requiring further abbreviation.

Step 5.  Add one more counter in the 1’s place (2020-place) square in the bottom row. This may cause a “chain reaction” that “carries” into squares to the left, requiring further abbreviation.

Step 6.  The desired answer can now be obtained by converting the abbreviated difference back to a decimal number, except that you must ignore the farthest left counter (which may already have “fallen” off the left side of the board).

Example: That 116 – 84 = 32 is illustrated below.

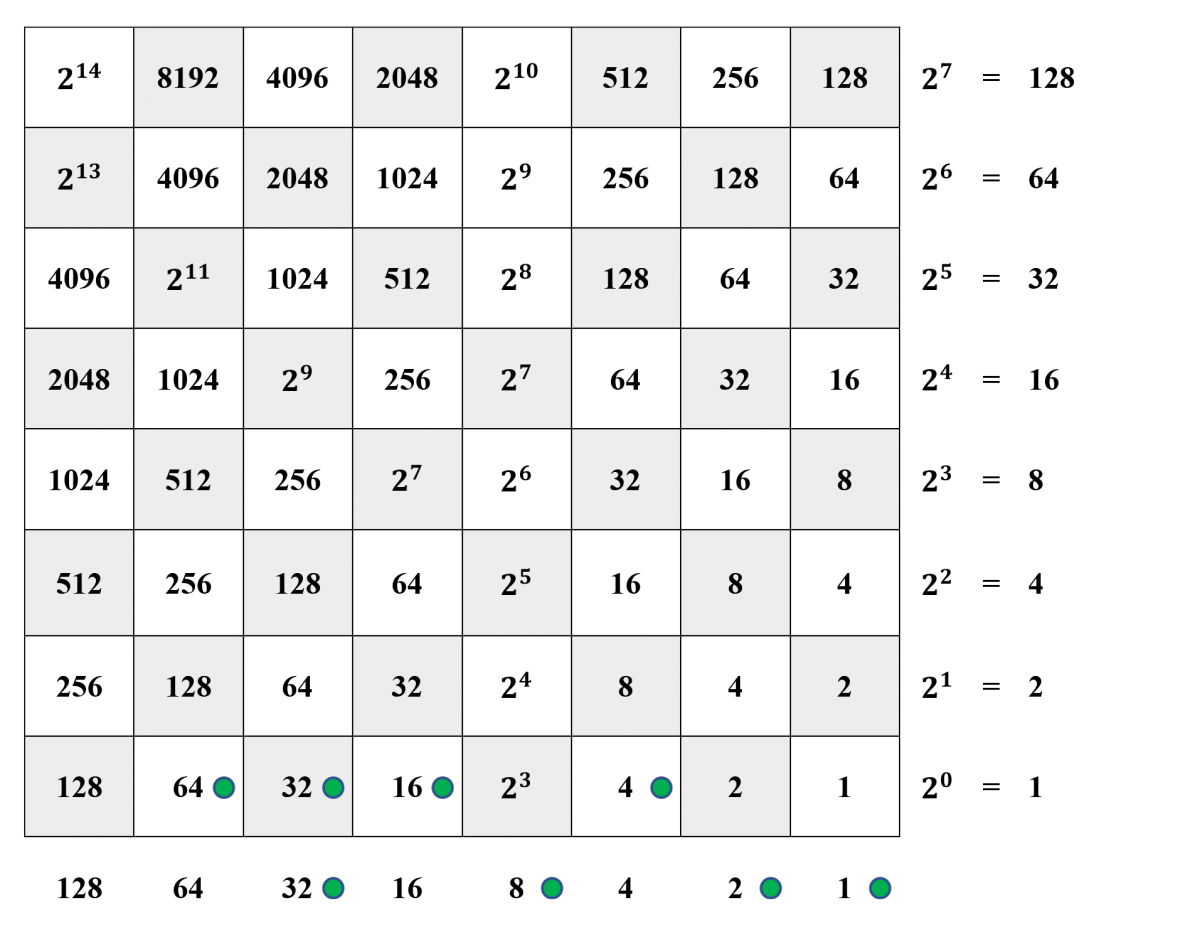
Steps 1 and 2. The larger integer, 116, decomposed as

116=26+25+24++22++=64+32+16++4++,116=26+25+24++22++=64+32+16++4++,is represented by counters in the bottom horizontal row. Now we decompose 84 as

84=26++24++22++=64++16++4++,84=26++24++22++=64++16++4++,and write its complement

25++23++21+20=32++8++2+1.25++23++21+20=32++8++2+1.The complement is represented in the margin below the bottom horizontal row.

The binary complement of a positive integer is sometimes called the “1’s complement” because one can compute it by interchanging 0’s and 1’s in the binary-digit representation of the positive integer. For instance:

64        32        16         8         4         2         1

  1          0          1         0         1         0         0     ←← Binary-digit representation for 84

  0          1          0         1         0         1         1     ←← 1’s complement of 84

The binary complement of 84 is therefore 32 + 8 + 2 + 1.

Step 3. Combine all of the counters in the bottom horizontal row:

Step 4. Abbreviate the row from right to left. Note that there is now a counter in the 128 or 2727 place:

Step 5.  Add +1; that is, add one more counter to the 1’s place, and …

… abbreviate the row from right to left:

Step 6.  Now, ignoring the farthest left counter, the difference can be read from this row as 116 – 84 = 32.

Next: multiplication on the chessboard calculator

Step 1. Place counters representing one factor along the bottom (horizontal) margin and counters for the other along the right-hand (vertical) margin. 

Step 2. Place a counter in each square on the board representing the intersection of a column for which there is a counter in the bottom (horizontal) margin with a row for which there is a counter in the right-hand (vertical) margin. The square represents the product of those two values.

Step 3. Remove the counters representing the factors from both margins.

Step 4. Slide all counters on the board along their (SW-NE) equivalence lines down to the bottom horizontal row. (This is how a bishop moves in chess.)

Step 5. Abbreviate the bottom horizontal row from right to left, removing every two counters in a square and placing one counter in the square to its left. This process often causes a “chain reaction” that “carries” into squares to the left, requiring further abbreviation.

Step 6. The desired decimal product can now be obtained by converting the abbreviated product back to a decimal number. 

Note that products represented on our 8×88×8 binary chessboard can be no larger than 255.

Example: That 18⋅13=23418⋅13=234 is illustrated below.

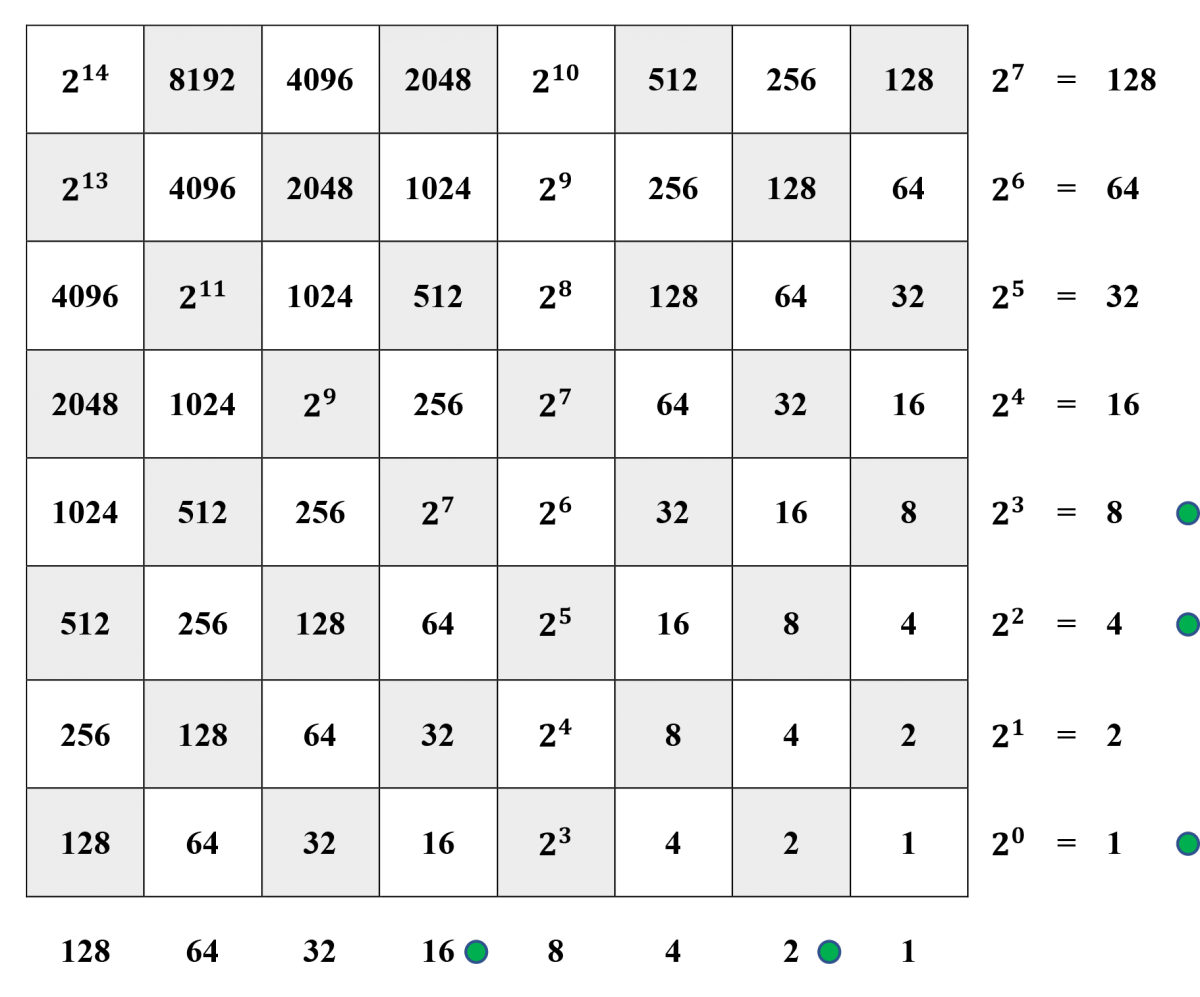
Step 1. The factor 18=16+218=16+2 is represented along the bottom margin and the factor 13=8+4+113=8+4+1 is represented along the right-hand margin.

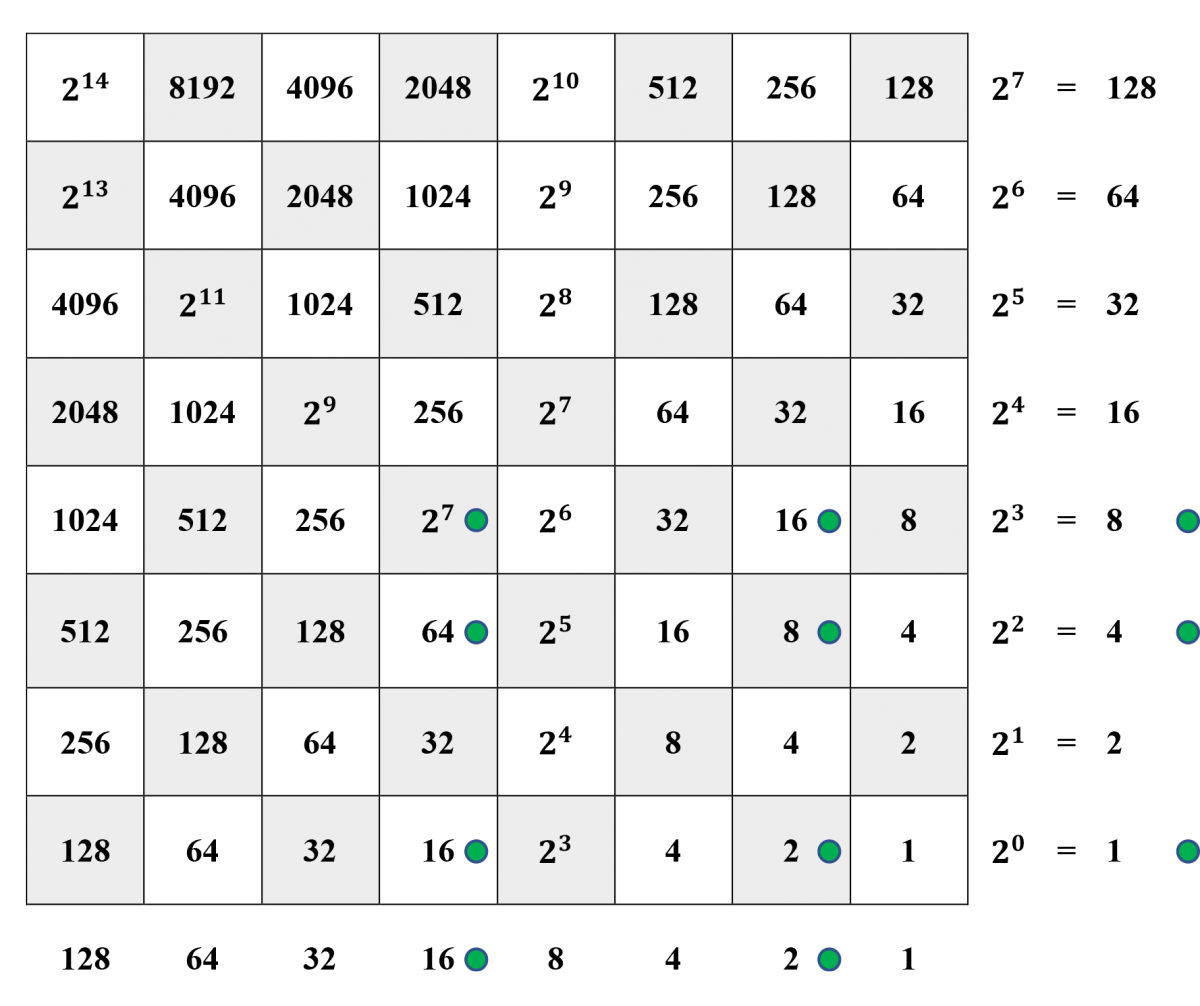
Step 2. Counters are placed at the intersections of columns and rows for which there are counters both along the bottom margin and along the right-hand margin. For instance, a counter is placed at the intersection of the column labeled 16 at the bottom and the row labeled 4 at the right. The intersection of this column and row is a square labeled 64, and you should check that 16⋅4=64.16⋅4=64.

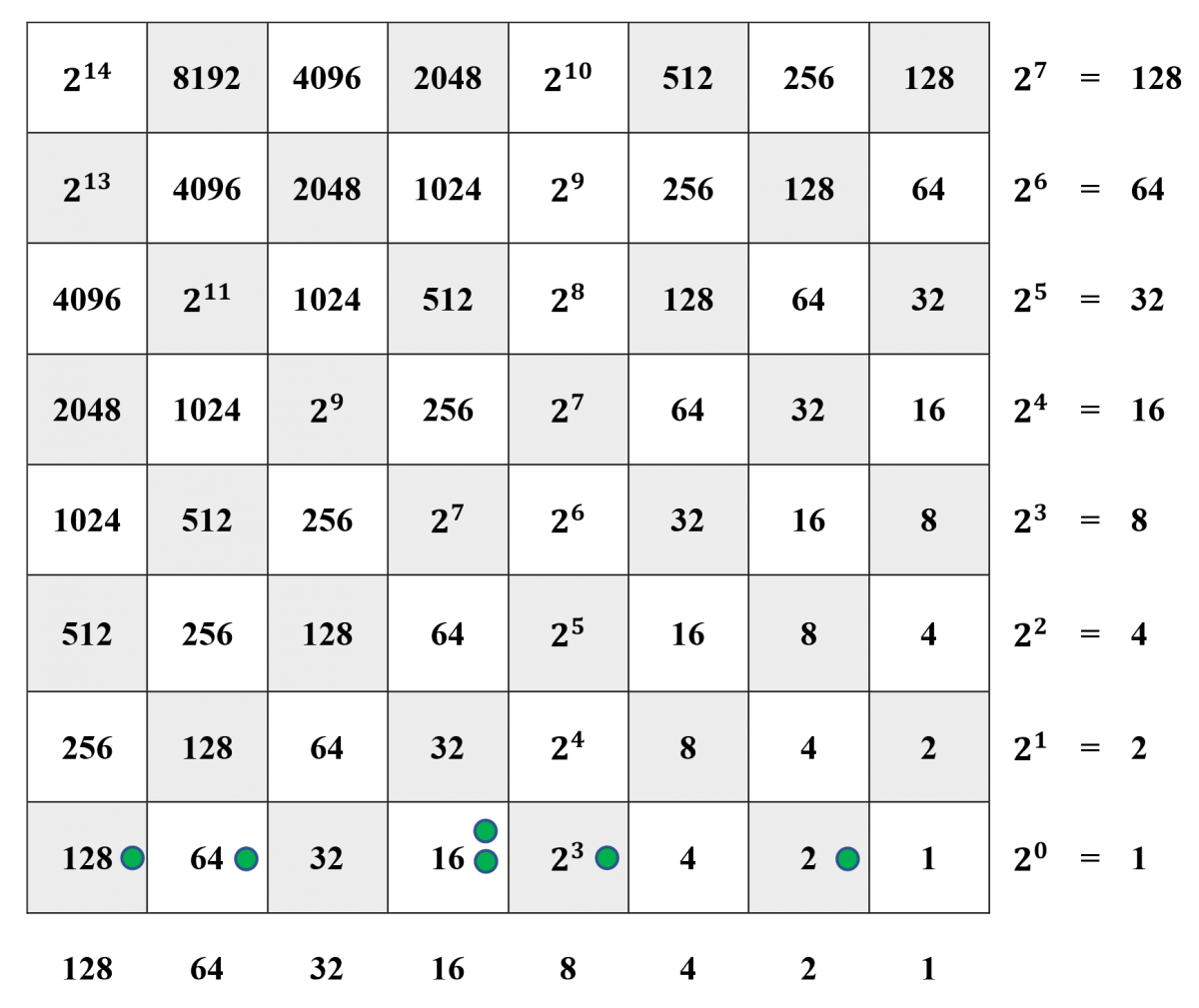
Steps 3 and 4. Counters have been cleared from the bottom (horizontal) and right-hand (vertical) margins. Counters on the board have been slid down their equivalence lines to the bottom horizontal row. For instance, the only counter at a square labeled 64 has been slid along the 64-equivalence line to the 64-square in the bottom row. Likewise, the two counters that were in squares along the 16-equivalence line now both sit in the 16-square in the bottom row.

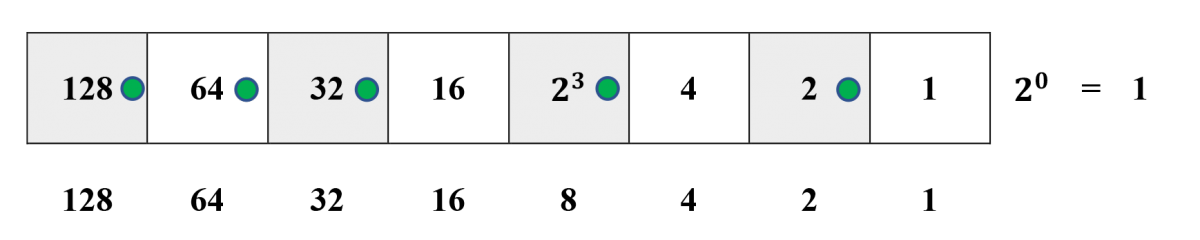
Steps 5 and 6. The bottom row has been abbreviated from right to left, leaving a row from which we can read

18⋅13=128+64+32+8+2=234.18⋅13=128+64+32+8+2=234.The reader may wish to carry out the multiplication 6⋅15,6⋅15, an example requiring extensive carries in the abbreviation process.

In preparation for extracting square roots on the chessboard calculator, it is worth noting here that, after obtaining 18⋅13=(16+2)(8+4+1)18⋅13=(16+2)(8+4+1) in Step 1 above, Step 2 amounts to an application of the distributive law to obtain:

(16+2)(8+4+1)=16⋅8+2⋅8+16⋅4+2⋅4+16⋅1+2⋅1,(16+2)(8+4+1)=16⋅8+2⋅8+16⋅4+2⋅4+16⋅1+2⋅1,with the six products on the right-hand side of this equation necessarily arranged in a 3 row by 2 column rectangle on the chessboard. More specifically, removal of one entire row and two entire columns from the second board shown above would result in a 3 row by 2 column rectangle consisting of six contiguous squares with counters in them.

Next: division on the chessboard calculator 

Step 1. Represent the dividend in the horizontal margin and the divisor in the vertical margin.

Step 2. Place a counter on the largest number in the first column (farthest column to the right) that when multiplied by the divisor is less than or equal to the dividend.

Step 3. Multiply that number by the divisor and subtract the product from the dividend. Replace the dividend (in the horizontal margin) with this result, which will become the current dividend.

Step 4. Repeat steps 2 and 3 with the current dividend until you can no longer do so.

Step 5. The sum of the chips in the first column is the quotient. The current dividend is the remainder.

Example: That 100100 divided by 77 results in a quotient of 1414 and a remainder of 22 is illustrated below.

Steps 1 and 2. The dividend 100100 is represented in the horizontal margin and the divisor 77 in the vertical margin. Since 7⋅16>100,7⋅16>100, but 7⋅8≤100,7⋅8≤100, a counter has been placed on the 8-square in the right-hand column.

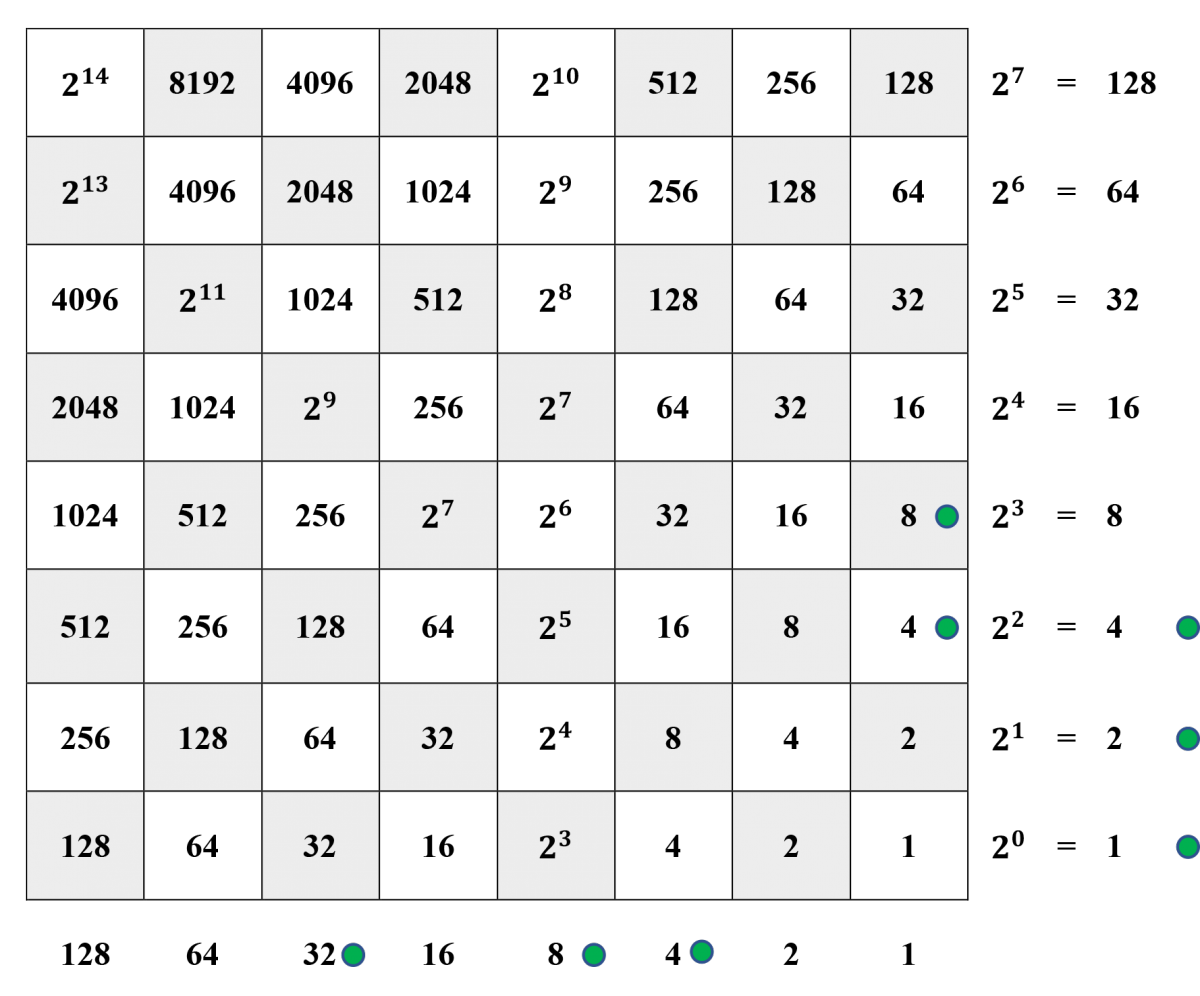
Steps 3 and 4. Since 7⋅8=56,7⋅8=56, the current dividend is 100−56=44,100−56=44, as represented in the horizontal margin. Furthermore, since 7⋅8>44,7⋅8>44, but 7⋅4≤44,7⋅4≤44, a counter has been placed on the 4-square in the right-hand column.

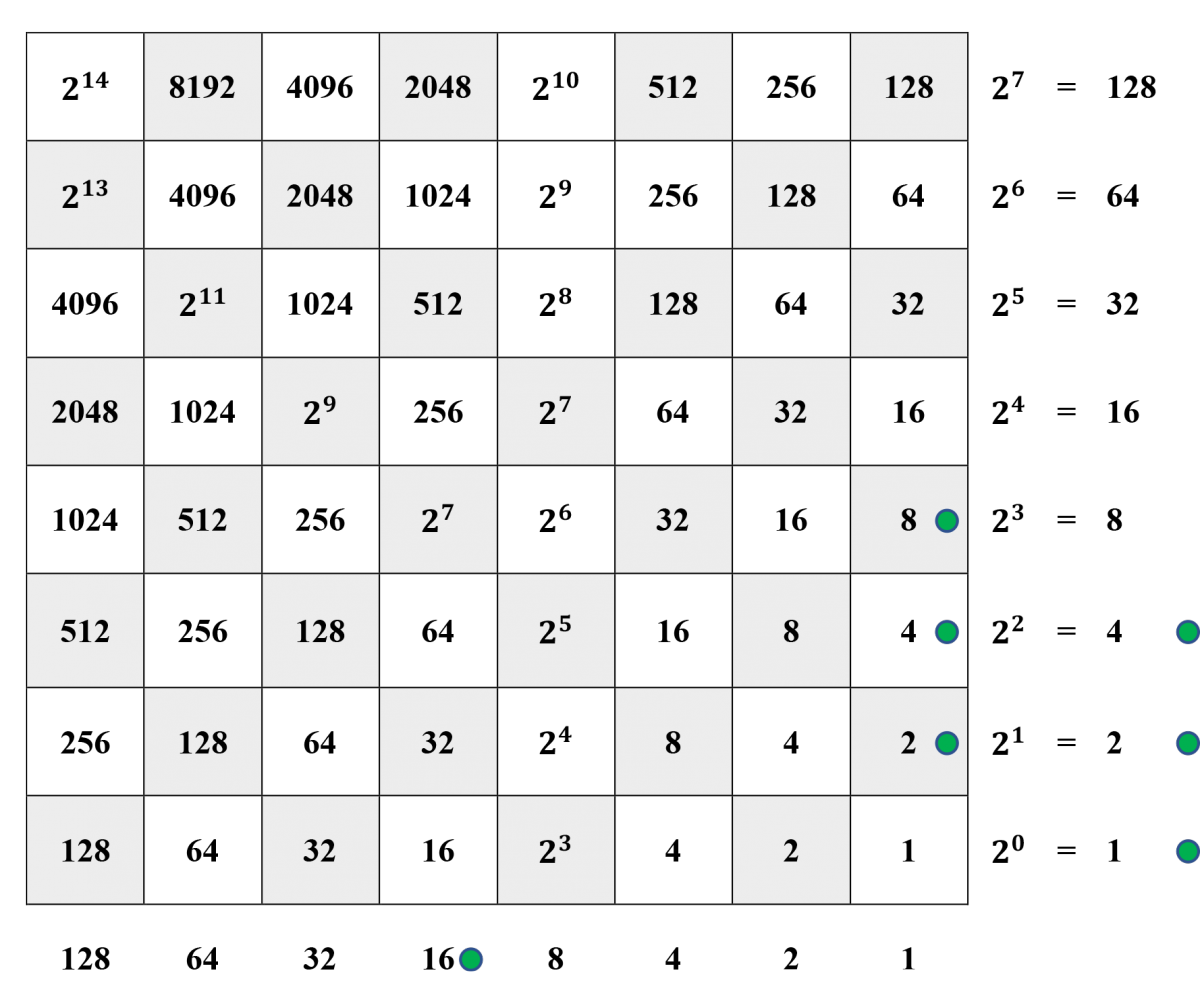
Step 4. Since 7⋅4=28,7⋅4=28, the current dividend is 44−28=16,44−28=16, as represented in the horizontal margin. Furthermore, since 7⋅4>16,7⋅4>16, but 7⋅2≤16,7⋅2≤16, a counter has been placed on the 2-square in the right-hand column.

Hey. If you see this, you either got lucky and this caught your eye as something not boring, or you actually read this far. If you are the first person, whatever. If you are the second type, please go see a psychiatrist. You are not mentally stable. Either way, go comment “GREEN PLAYDOUGH ON TOP” If you see this.

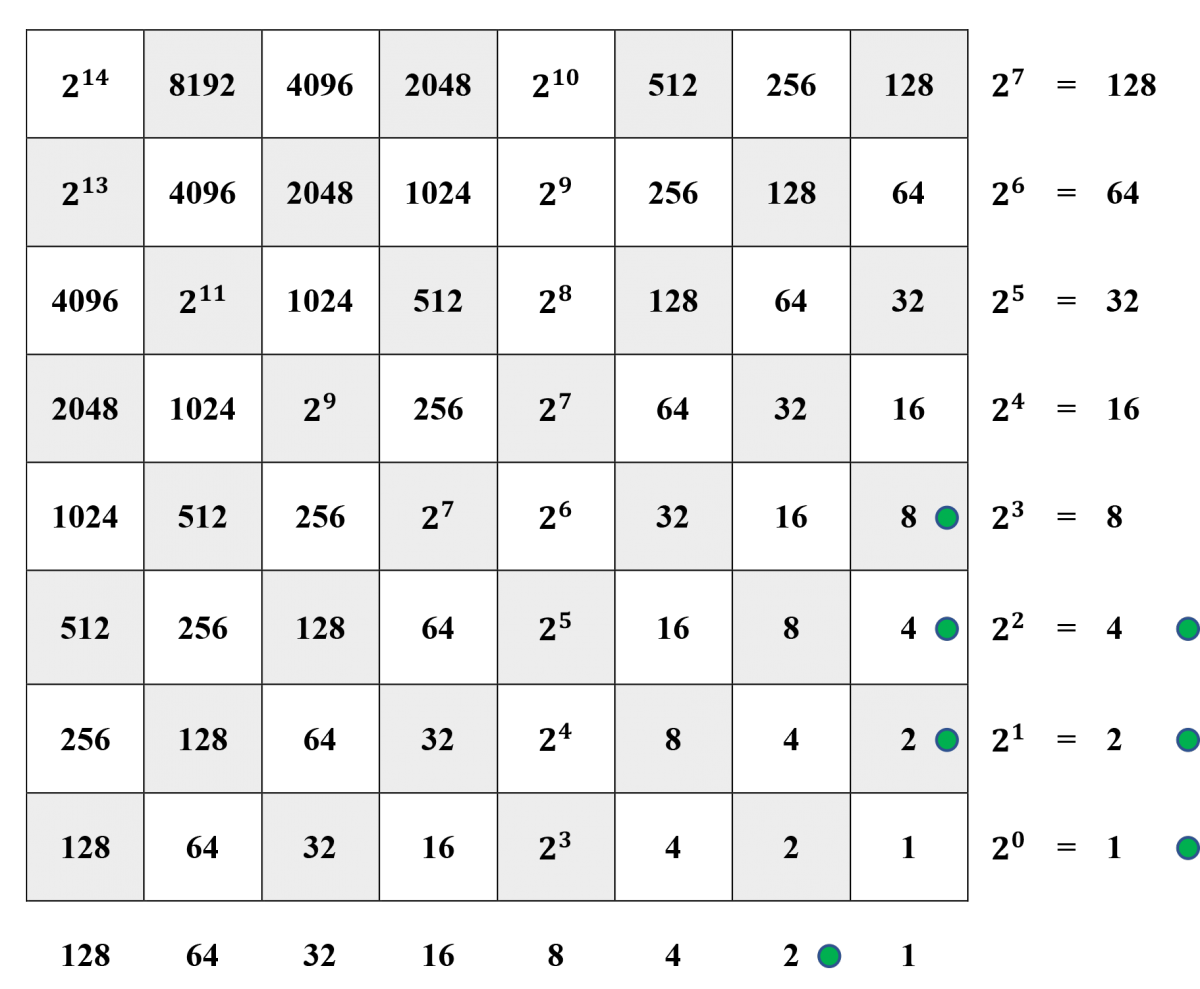
Step 4, continued. Since 7⋅2=14,7⋅2=14, the current dividend is 16−14=2,16−14=2, as represented in the horizontal margin. Since 7⋅1>2,7⋅1>2, we cannot continue.

Step 5. We conclude that dividing 100100 by 77 results in a quotient of 8+4+2=148+4+2=14 and a remainder of 2.

You just scrolled here, didn’t you?

Don’t lie to yourself. You just scrolled until you hit the bottom. I don’t blame you, reading that stuff makes me want to throw up. Anyways, you are at the end now. Want a good boy award or something? Well, I don’t have any, and I know none of you read anything, so whatever. There is actually 2 other pages about square roots and stuff, but I gave up pasting all of that.

John Napier’s Binary Chessboard Calculator – Simplified | Mathematical Association of America